个人技术博客

0%

默克尔树原理以及应用场景

发表于 分类于

前言：

​ hello大家好我是Monday，今天给大家带来一篇关于默克尔树的原理以及应用场景的文章。

一、默克尔树的原理和特点：

（1）哈希树（默克尔树）中，每个节点都标有一个数据块的加密哈希值

（2）（默克尔树）叶节点（leaf）包含存储数据或其哈希值，

（3）默克尔树是从下往上逐层计算，每个中间节点是根据相邻的两个叶子节点组合计算得出的，而根节点是根据两个中间节点组合计算得出的，所以叶节点是基础。因此，底层数据的任何变动，都会传递到其父节点，一直到树的根节点。

（4）哈希树（默克尔树）的特点
叶节点存储的是数据文件，而非叶节点存储的是其子节点的哈希值（Hash，通过SHA1、SHA256等哈希算法计算而来），这些非叶子节点的Hash被称作路径哈希值（可以据其确定某个叶节点到根节点的路径）,
叶节点的Hash值是真实数据的Hash值。因为使用了树形结构, 其查询的时间复杂度为 O(logn)，n是节点数量。

如图1所示：

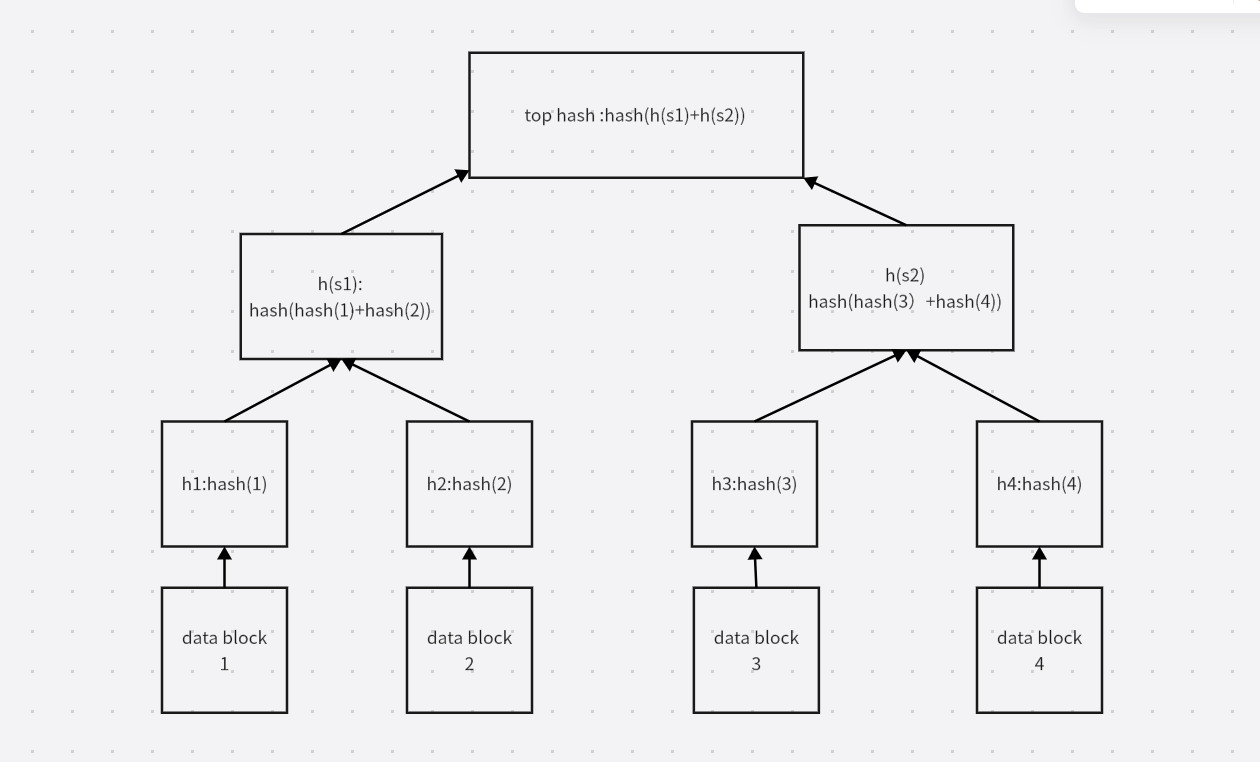
​ 图1

二，应用模式：
默克尔树的典型应用场景包括：
（1） 快速比较大量数据：当两个默克尔树根相同时，则意味着所代表的数据必然相同（哈希算法决定的）。
（2）快速定位修改：例如 图1，如果 D1 中数据被修改，会影响到H1，H(s1) 和 Top Hash。因此，沿着 Top Hash—> H(s1) —>H1，可以快速定位到发生改变的 D1；

（3）零知识证明：例如如何证明某个数据（D1……D4）中包括给定内容 D1，很简单，构造一个默克尔树，公布H2，H(s1)，H(s2)，Top Hash，D1拥有者可以很容易检测 D1存在，但不知道其它内容。

相对于 Hash List，默克尔树的明显的一个好处是可以单独拿出一个分支来（作为一个小树）对部分数据进行校验，这个很多使用场合就带来了哈希列表所不能比拟的方便和高效。正是源于这些优点，默克尔树常用于分布式系统或分布式存储中

举例说明(1)：

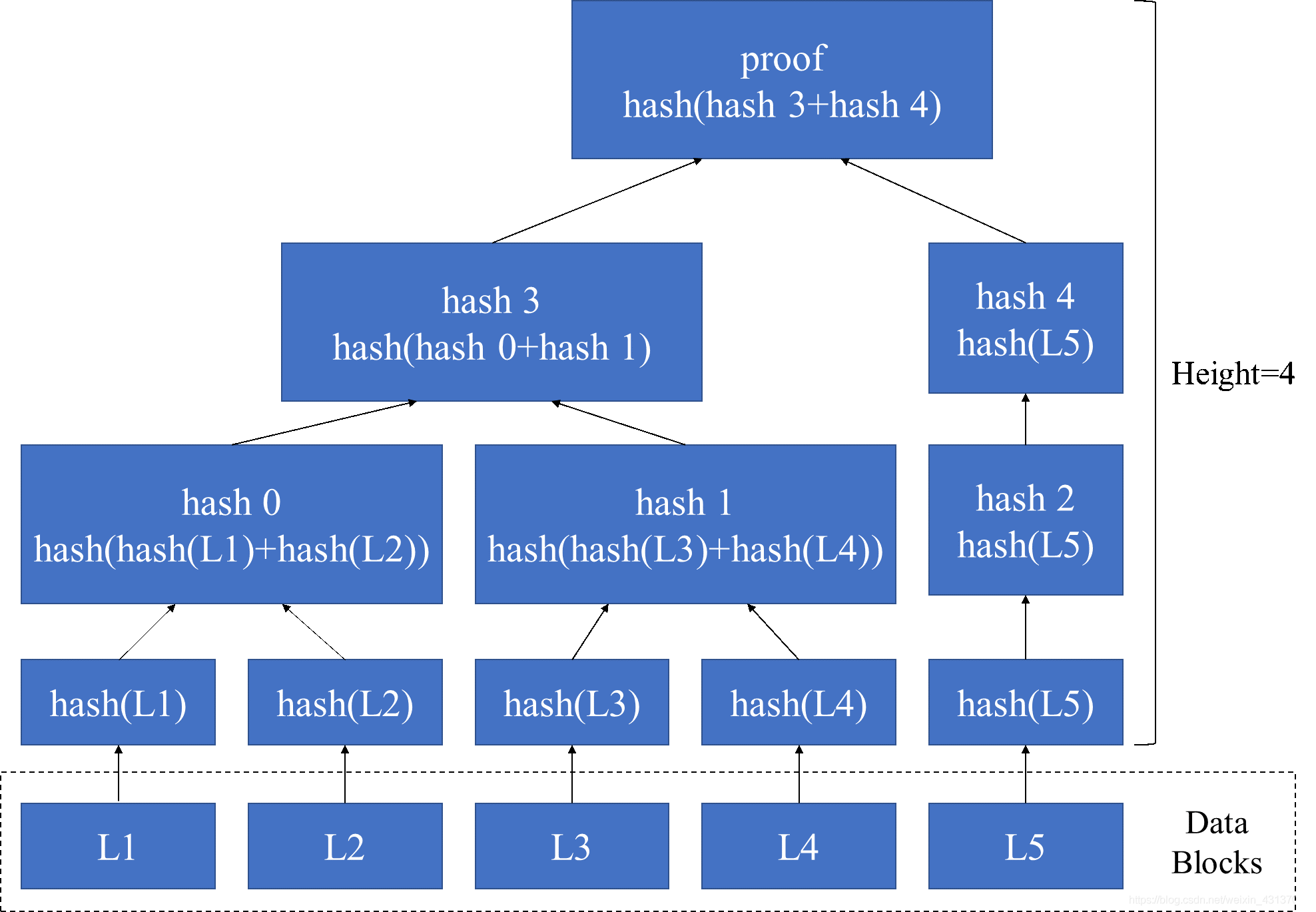
​ proof可以用来检验数据的完整性和正确性，即一个data block的改动或缺失，就会导致proof的改变。

同时，merkle树可以用于数据传输，同时从多个机器下载数据的不同部分，可以提高效率。常见的迅雷的p2p下载，即采用这种模式，从多台机器下载，并用merkle tree检验数据的完整性和正确性。

默克尔树是区块链技术中用于保障数据不被篡改的重要安全手段之一，

举例说明(2)：

​ 默克尔证明是一种经典技术,用于证明交易存在于区块链的某个区块中,是实现轻客户端的关键技术。我们以Wecross跨链项目中使用的数据互信机制来介绍默克尔证明。

假设两个用户甲和乙要在两条不同区块链上完成资产交换，那么必须要有一种机制来保证两个用户都真实拥有所宣称的资产，否则任何一方的用户都可以使用伪造的链上资产去兑换对方有效的链上资产。数据互信机制就是要解决这种跨链场景下的数据可信问题，它基于默克尔证明机制来实现，使得一方在不需要获取另一方区块链全量数据的情况下，仍然能够快速证明另一方区块链上特定数据的真实存在性。

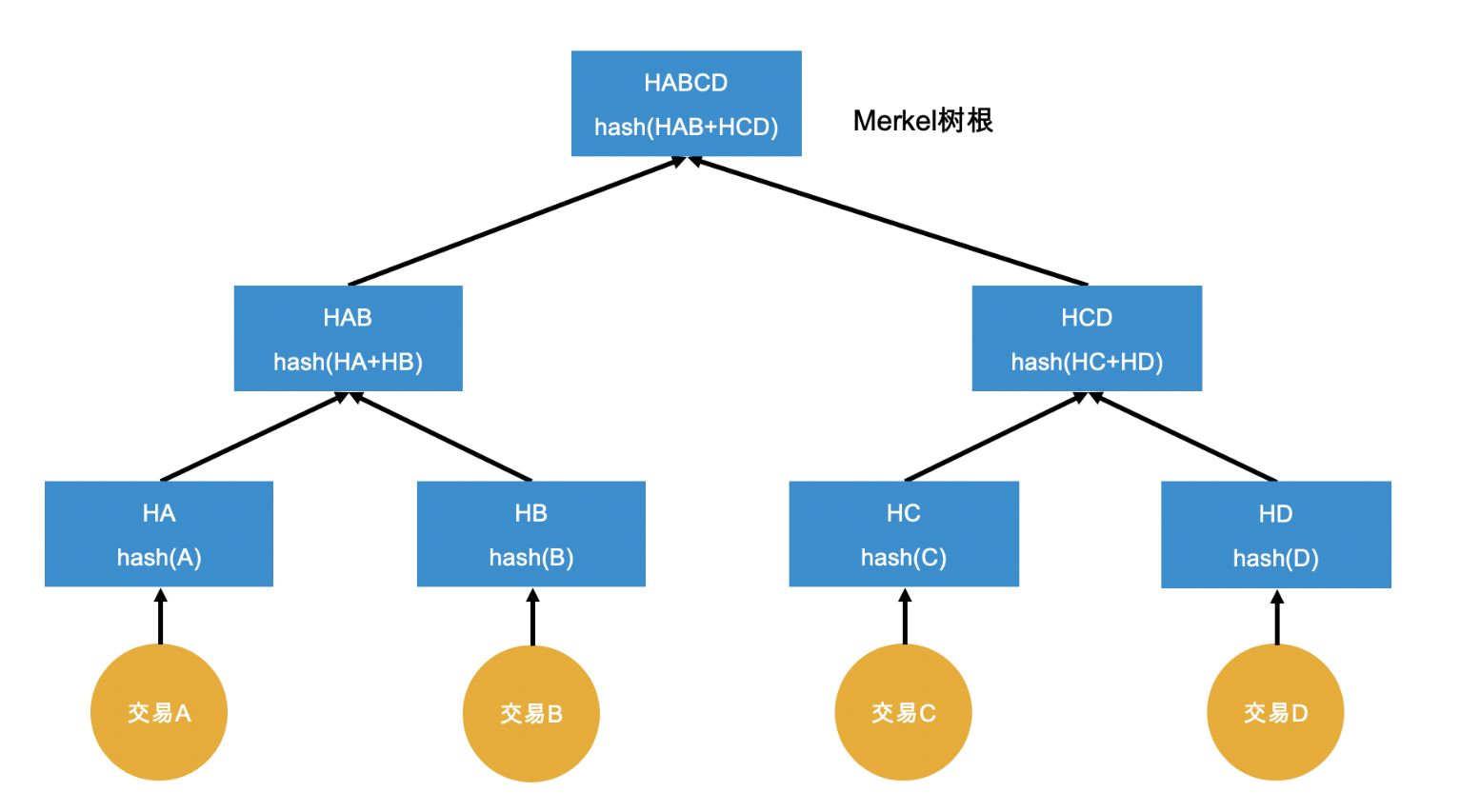
假设上图是区块 X 的默克尔树结构，如果要验证交易D是否在区块X中，无需获取整个区块X，只需要提供交易D，H_AB，H_C，以及默克尔根则可。具体过程如下：

根据交易 D 计算哈希，得到 H_D。

根据 H_C 和 H_D 计算哈希，得到 H_CD。

根据 H_AB 和 H_CD 计算哈希，得到 H_ABCD。

对比 H_ABCD 和默克尔根，如果相同，则证明区块 X 存在交易 D,，否则说明不存在。

四、Merkle树算法解析及python实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import hashlib  # 用于哈希值计算
#(代码来源于网络)

# 默克尔树节点类的定义
class MerkleNode(object):
    def __init__(self, left=None, right=None, data=None):
        self.left = left
        self.right = right
        # data中保存着哈希值
        self.data = data


# 以递归的方式构建默克尔树
def createTree(nodes):
    list_len = len(nodes)
    if list_len == 0:
        return 0
    else:
        while list_len % 2 != 0:
            nodes.extend(nodes[-1:])
            list_len = len(nodes)
        secondary = []
        # 两两合并节点，并计算其哈希值
        for k in [nodes[x:x + 2] for x in range(0, list_len, 2)]:
            d1 = k[0].data.encode()
            d2 = k[1].data.encode()
            md5 = hashlib.md5()
            md5.update(d1 + d2)
            newdata = md5.hexdigest()
            node = MerkleNode(left=k[0], right=k[1], data=newdata)
            secondary.append(node)
        if len(secondary) == 1:
            return secondary[0]
        else:
            return createTree(secondary)


# 利用广度优先搜索算法对节点数据进行遍历
def BFS(root):
    print('开始广度优先搜索，构建默克尔树...')
    i = 0
    queue = []
    queue.append(root)
    while (len(queue) > 0):
        e = queue.pop(0)
        i += 1
        # print("Hash Value:"+str(i),e.data)
        if e.left != None:
            queue.append(e.left)
        if e.right != None:
            queue.append(e.right)
        print("Hash value:" + str(i), e.data)


if __name__ == "__main__":
    blocks = ['node1', 'node2', 'node3', 'node4']  # 示例数据，包含4个节点
    nodes = []  # 节点初始化
    print("节点哈希值：")
    for element in blocks:  # 遍历示例数据
        md5 = hashlib.md5()  # 摘要算法
        md5.update(element.encode())
        d = md5.hexdigest()  # 计算节点的信息摘要
        nodes.append(MerkleNode(data=d))  # 添加至默克尔树节点中
        print(element + ":", d)
    root = createTree(nodes)  # 创建默克尔根节点
    BFS(root)  # 基于BFS算法构建默克尔树并输出所有的哈希(摘要)

结束语：

​ 今天的分享就到这里了，欢迎大家关注微信公众号菜鸟童靴